题目描述

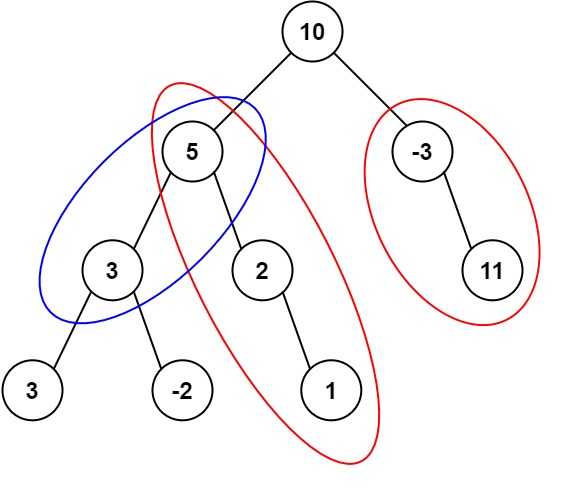
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

题目分析

前序遍历，记录前面走过的结点，以当前结点为终点，向前累加。但会发现在计算累加和这里存在很多重复计算，时间复杂度 O(n * n).
设从根结点到当前结点的和是 sum，使用 HashMap 存储以根结点为起点的前缀和。由于存在负数的结点值，所以同一个前缀和可能会存在多个。
对于一个结点，如果它是 targetSum 路径的终点，那么 targetSum + 前缀和 = sum。因此只要查看 map 中是否存在 sum – targetSum 即可。
时间复杂度 O(n)

Java

private int count = 0;
private HashMap<Long, Integer> preSum;

// 前序遍历 + 前缀和
// 时间复杂度 O(n)
public int pathSum(TreeNode root, int targetSum) {
    count = 0;
    preSum = new HashMap<>();
    preSum.put(0L, 1);
    dfs(root, targetSum, 0);
    return count;
}

private void dfs(TreeNode root, int targetSum, long sum) {
    if (root == null) {
        return;
    }
    sum += root.val;
    count += preSum.getOrDefault(sum - targetSum, 0);
    preSum.put(sum, preSum.getOrDefault(sum, 0) + 1);
    dfs(root.left, targetSum, sum);
    dfs(root.right, targetSum, sum);
    preSum.put(sum, preSum.getOrDefault(sum, 0) - 1);
}

Kotlin

private val preSum = HashMap<Long, Int>()
private var count = 0

fun pathSum(root: TreeNode?, targetSum: Int): Int {
    count = 0
    preSum.clear()
    preSum[0L] = 1
    dfs(root, targetSum, 0)
    return count
}

private fun dfs(root: TreeNode?, targetSum: Int, sum: Long) {
    if (root == null) {
        return
    }

    val newSum = sum + root.`val`
    count += preSum.getOrDefault(newSum - targetSum, 0)
    preSum[newSum] = preSum.getOrDefault(newSum, 0) + 1
    dfs(root.left, targetSum, newSum)
    dfs(root.right, targetSum, newSum)
    preSum[newSum] = preSum.getOrDefault(newSum, 0) - 1
}