这是小学期的作业,简单的总结一下。
开发者:关浩博、张存涛、张迪
一、开发环境
操作系统:Windows 10 64位
IDE:Dev-C++ 5.11
二、引言
数独作为一种游戏,有着悠久的历史,一个完整的数独要求在一个9*9的棋盘上,数独里面包含九个宫,每个宫里面有九个小格,游戏者需要填满从“1”到“9”共9个数字,保证每行,每列,每个宫格内部没有相互重复的数字,完成所有宫格内的数字填写。样例如下图所示
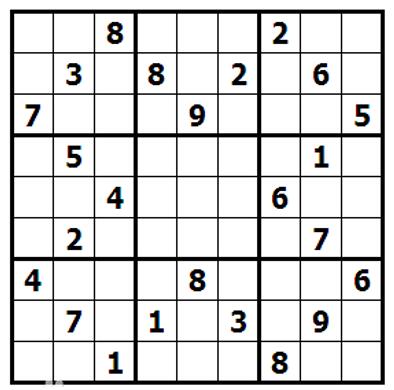
三、需求分析
我们初步设计了“读入数独,程序判断”、“输入题目,程序求解”、“输入题目,输入答案”、“程序出题,输入答案”以及“游戏介绍”和“开发者信息”等功能。
“读入数独,程序判断”即用户输入一个9*9的数独,程序来判断是否是一个正确的数独。“输入题目,程序求解”即用户输入一个题目,程序填写好其中一个解,如果无解则提示用户输入错误。“输入题目,输入答案”即为用户输入一个题目,用户自己完成填写,用于两人相互出题并相互解答。“程序出题,输入答案”即程序自动生成题目用户来完成解答。
四、流程图
4.1 主函数
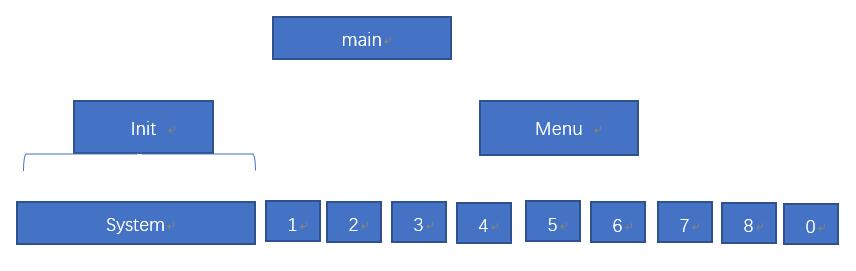
4.2 子函数
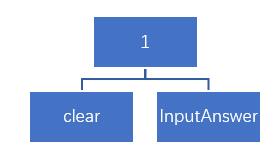
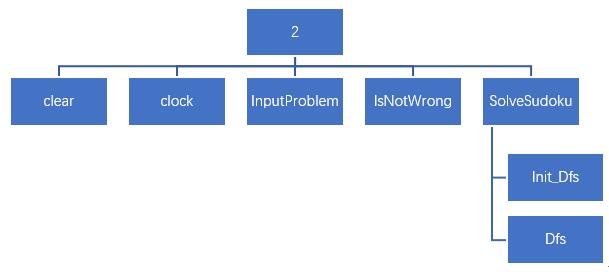

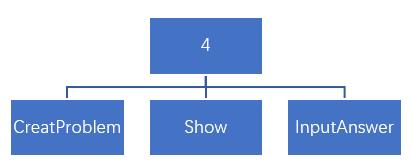
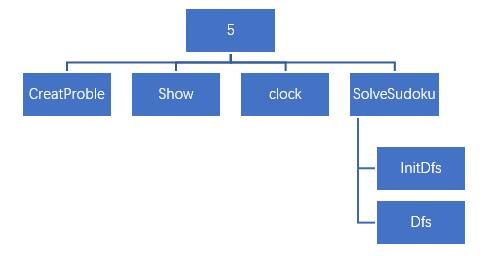
五、核心算法分析
5.1 题目生成算法
基本思想:使用宫变换法生成数独终盘,再随机去除若干个数字,即可得到一个有解的数独题目。
数独分为9个宫编号为0到8,先随机填写其中中间的宫格,即第4个宫格,使第4个宫有数字1到9且每个数字仅出现一次,然后通过矩阵行列变换由第4个宫格生成其他的8个宫的数字。具体的可以参考下面的代码。
之后随机删除若干个数字即可。
优点:采用宫变换来完成题目的生成,效率极高。同时在扣除数字的时候,因为从完整的数独进行扣除,所以至少有一个解,不需要担心无解的情况,省去了判断的条件,让运行时间大大减少。
缺点:生成的数独终盘的个数是9的阶乘,存在一些数独终盘是不可能生成的;随机删除数字后会出现一题多解的情况。
void Sudoku::CreatProblem() //使当前数独成为一个有解的数独题目
{
Clear();
int x, y;
/*中间格第4格随机值 */
for (int i = 3; i <= 5; i++)
{
for (int j = 3; j <= 5; j++)
{
do
{
x = rand() % 9 + 1;
} while (countGe[4][x]);
num[i][j] = x;
countRow[i][x] = countCol[j][x] = countGe[4][x] = 1;
}
}
/*填充第3格 */
for (int i = 3; i <= 5; i++)
{
for (int j = 0; j <= 2; j++)
{
num[i][j] = num[(i - 1 + 3) % 3 + 3][j + 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[3][x] = 1;
}
}
/*填充第5格 */
for (int i = 3; i <= 5; i++)
{
for (int j = 6; j <= 8; j++)
{
num[i][j] = num[(i + 1 + 3) % 3 + 3][j - 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[5][x] = 1;
}
}
/*填充第1格 */
for (int i = 0; i <= 2; i++)
{
for (int j = 3; j <= 5; j++)
{
num[i][j] = num[i + 3][(j - 1 + 3) % 3 + 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[1][x] = 1;
}
}
/*填充第7格 */
for (int i = 6; i <= 8; i++)
{
for (int j = 3; j <= 5; j++)
{
num[i][j] = num[i - 3][(j + 1 + 3) % 3 + 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[7][x] = 1;
}
}
/*填充第0格 */
for (int i = 0; i <= 2; i++)
{
for (int j = 0; j <= 2; j++)
{
num[i][j] = num[i + 3][(j - 1 + 3) % 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[0][x] = 1;
}
}
/*填充第6格 */
for (int i = 6; i <= 8; i++)
{
for (int j = 0; j <= 2; j++)
{
num[i][j] = num[i - 3][(j + 1 + 3) % 3];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[6][x] = 1;
}
}
/*填充第2格 */
for (int i = 0; i <= 2; i++)
{
for (int j = 6; j <= 8; j++)
{
num[i][j] = num[i + 3][(j - 1 + 3) % 3 + 6];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[2][x] = 1;
}
}
/*填充第8格 */
for (int i = 6; i <= 8; i++)
{
for (int j = 6; j <= 8; j++)
{
num[i][j] = num[i - 3][(j + 1 + 3) % 3 + 6];
x = num[i][j];
countRow[i][x] = countCol[j][x] = countGe[8][x] = 1;
}
}
size = 81;
while (size > 25)//保留25个数字
{
do
{
x = rand() % 9;
y = rand() % 9;
} while (num[x][y] == 0);
int t = num[x][y];
num[x][y] = 0;
size--;
countRow[x][t] = countCol[y][t] = countGe[x / 3 * 3 + y / 3][t] = 0;
}
}
5.2 数独求解算法
分析
通过数独的定义不难发现,用递归的思想(回溯法)能很好的解决这个问题。但是简单的回溯在程序的运行时间上会很长。首先我们来分析一下简单的回溯法所需要的时间。以20个格有数字为例,对于其他的61个格,如果想求出所有的解,最坏的情况下要递归9的61次方,在这个数量级下,我们可以明显的观察到程序卡的情况。
为了解决再盲目情况下的回溯,时间复杂度太大的问题,参考了《基于自定义信息熵解决数独难题》论文中提出的信息熵和逆熵的原理,对此算法进行优化,可以实现求解数独所用的时间有了较大的减少。以下是我们小组对求解时间的统计。
可能由于统计的数独个数较少有较大的误差,但是基于信息熵和逆熵的解决方案是可行的。
| 难度等级 | 简单回溯(平均时间) | 基于信息熵(平均时间) |
|---|---|---|
| 容易 | 500ms | 300ms |
| 较难 | 1000ms | 320ms |
| 困难 | 2000ms | 350ms |
具体优化
(1)、首先我们来看一下简单回溯的具体步骤:
步骤1:从数独的第一个格开始
步骤2:判断当前元素是否有数字,有则到下一个格。无,从1到9尝试填数。
然后递归下一格。
步骤三:判断数独是否已填满,是,该递归分支结束。否,继续填下一个格。
让我们来看一下伪代码:
backTracking(int index){
if(index == 81){
格子已经填满,输出结果
}
//x,y表示格子的坐标
x = index % 9;
y = index / 9;
if(grid(x, y)的数字为题目的信息){
backTracking(index+1); //题目给出的数字是确定的,没必要搜索
}
for(i=1; i<=9 ;i++){
if(isLegal(x, y, i)){ //逐个数字试探其合法性
grid(x, y) = i;
backTracking(index+1);
grid(x, y) = 0;
}
}
}
(2)、其次让我们来看一下基于信息熵的优化
步骤1:从所有空的格中取出熵最小的。
步骤2:从1到9开始尝试填数,递归下一个格。
步骤3:直到所有空的格的熵降为0。该递归分支结束。
代码
bool Sudoku::Dfs() //深度优先搜索,为SolveSudoku函数服务
{
int max = 0, mod = 0;
for (int i = 0; i <= 80; i++)
{
if (count_max[max] < count_max[i])
max = i;
}
if (count_max[max] == -1)
return true;
for (int i = 1; i < 10; i++)
{
if (CellIsOK(max, i))
{
num[max / 9][max % 9] = i;
countRow[max / 9][i] = 1;
countCol[max % 9][i] = 1;
countGe[max / 9 / 3 * 3 + max % 9 / 3][i] = 1;
mod = count_max[max];
count_max[max] = -1;
if (Dfs())
return true;
num[max / 9][max % 9] = 0;
countRow[max / 9][i] = 0;
countCol[max % 9][i] = 0;
countGe[max / 9 / 3 * 3 + max % 9 / 3][i] = 0;
count_max[max] = mod;
}
}
return false;
}
该函数调用递归的函数实现深度搜索,每一次循环,先比较熵的大小,在81个数字里面挑选出熵最大的数字,并判断,加入熵最大的数字里面已经填满了数字则证明数独已经完成,返回true,然后层层返回,得到最终的结果true。每一次深度搜索前要记录对应最大的熵,赋值给对应的最大的熵count_max[max],以此来修改对应的“-1”。并将结果存储到s2里面,并传递出来。
总结:基于信息熵求解数独的思想,与人工求解数独的思想类似。每次从所有格中从1到9可以用的最少数出发,可以大大减少递归的分支。从而使解数独所用的时间达到最短。
六、其他函数分析
6.1 Clear函数
void Sudoku::Clear() //清除数据
{
memset(num, 0, sizeof(num)); //给81个数字赋初值0
memset(countRow, 0, sizeof(countRow)); //赋值为0
memset(countCol, 0, sizeof(countCol)); //赋值为0
memset(countGe, 0, sizeof(countGe)); //赋值为0
size = 0; //初始非0元素个数为0
}
Clear函数实现了对每个变量的清空,对九宫格内所有数字的清空,给三个需要维护的数组清空(行维护数组,列维护数组,宫维护数组),将size即非零元个数清零。
6.2 CellIsOK()函数
bool Sudoku::CellIsOK(int n, int key) //判断下标为n的点如果值为key,是否和同一行、列、格相冲突,冲突返回true,不冲突返回false
{
if (!countRow[n / 9][key] && !countCol[n % 9][key] && !countGe[(n / 9) / 3 * 3 + (n % 9) / 3][key])
return true;
return false;
}
6.3 IsOK()函数
bool Sudoku::IsOK() //判断数独是否完全正确(成立条件:size==81且符合数独的定义),正确返回true;不正确则返回false
{
if (size == 81 && IsNotWrong())
return true;
return false;
}
6.4 IsNotWrong()函数
bool Sudoku::IsNotWrong() //判断数独是否暂时没有错误(成立条件:size<=81且非0的数字都符合数独的定义),正确返回true;不正确则返回false
{
int m[10];
memset(m, 0, sizeof(m));
//行
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
if (num[i][j] != 0)
{
if (m[num[i][j]])
return false;
else
m[num[i][j]] = 1;
}
}
memset(m, 0, sizeof(m));
}
//列
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
if (num[j][i] != 0)
{
if (m[num[j][i]])
return false;
else
m[num[j][i]] = 1;
}
}
memset(m, 0, sizeof(m));
}
//小格
int x = 0, y = 0;
for (; x < 9; x += 3)
for (y = 0; y < 9; y += 3)
{
for (int i = x; i < x + 3; i++)
for (int j = y; j < y + 3; j++)
{
if (num[i][j] != 0)
{
if (m[num[i][j]])
return false;
else
m[num[i][j]] = 1;
}
}
memset(m, 0, sizeof(m));
}
return true;
}
6.5 Show()函数
void Sudoku::Show() //显示数独的81个数字
{
cout << " *************************************************************************" << endl;
for (int i = 0; i < 9; i++)
{
printf(" * %d %d %d %d %d %d %d %d %d *\n", num[i][0], num[i][1], num[i][2], num[i][3], num[i][4], num[i][5], num[i][6], num[i][7], num[i][8]);
}
cout << " *************************************************************************" << endl;
}
6.6 InitDfs()函数
void Sudoku::InitDfs() //深度优先搜索前对一些数组的初始化
{
memset(countx, 0, sizeof(countx));
memset(county, 0, sizeof(county));
memset(count3, 0, sizeof(count3));
memset(count_max, 0, sizeof(count_max));
for (int k = 0; k < 81; k++)
{
if (!num[k / 9][k % 9])
{
for (int i = 0; i < 9; i++)
{
if (num[k / 9][i] != 0)
{
countx[k]++;
}
}
for (int i = 0; i < 9; i++)
{
if (num[i][k % 9] != 0)
{
county[k]++;
}
}
for (int i = (k / 9) / 3; i < (k / 9) / 3 + 3; i++)
{
for (int j = (k % 9) / 3; j < (k % 9) / 3 + 3; j++)
if (num[i][j] != 0)
{
count3[k]++;
}
}
if (countx[k] > county[k])
count_max[k] = countx[k];
else
{
count_max[k] = county[k];
}
if (count3[k] > count_max[k])
count_max[k] = count3[k];
}
else
{
count_max[k] = -1;
}
}
}
七、命令行版本测试
主菜单共提供了9个功能:输入数独,程序判断、输入题目,程序求解、输入题目,输入答案、程序出题,输入答案、程序出题,程序求解、游戏统计数据、游戏规则介绍、开发者信息、退出游戏。
7.1 输入数独,程序判断
用户自行输入数独题目,程序判断是否是正确的数独。
正确结果:
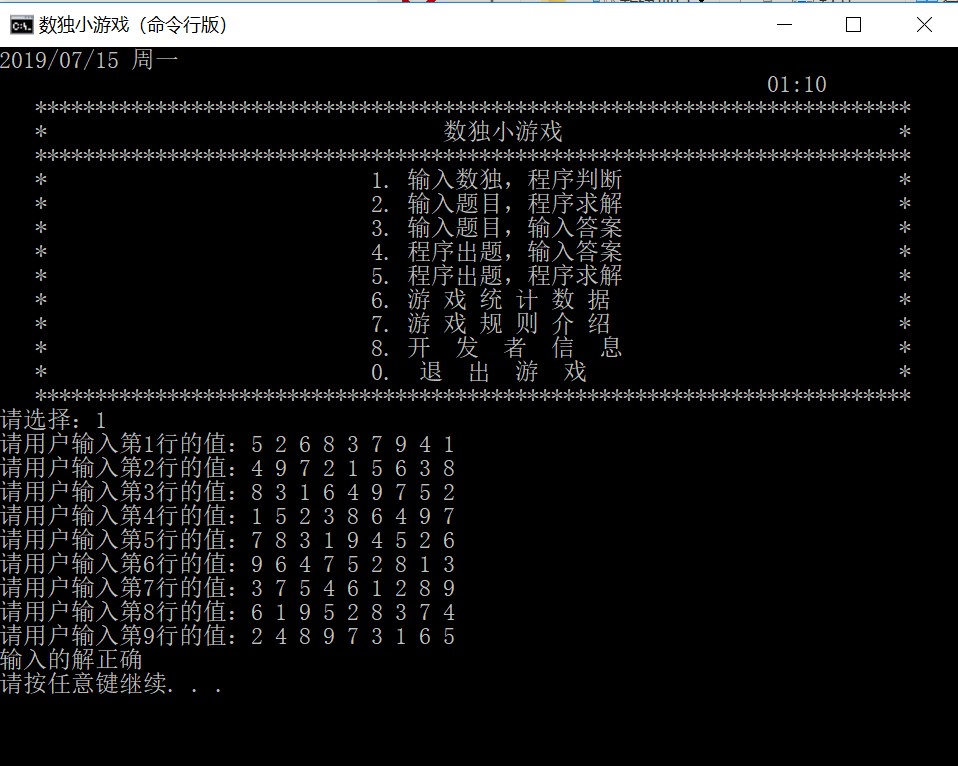
错误结果:
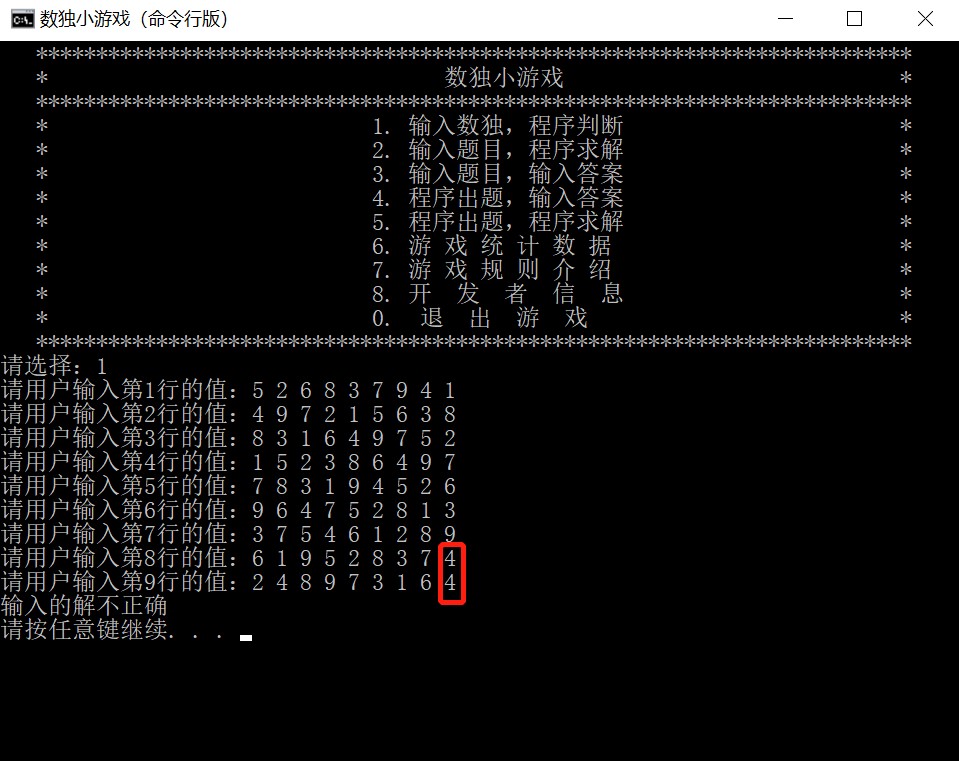
7.2 输入题目,程序求解
用户输入一个数独题目,空位置用数字0表示,程序完成求解过程。
有解:
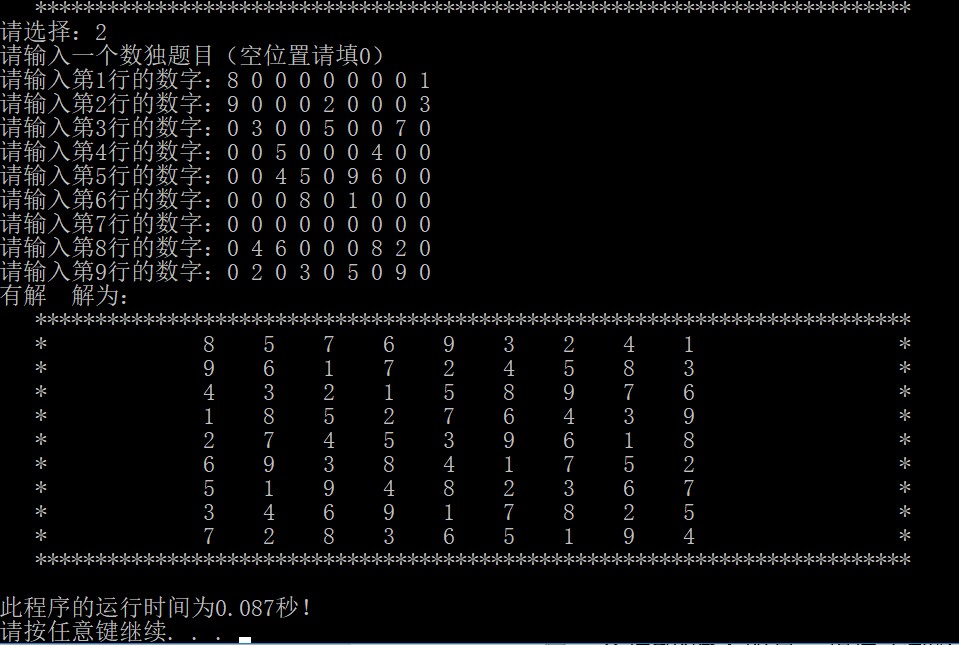
无解:

7.3 输入题目,输入答案
用户输入一个数独题目,空格用“0”表示,自行完成求解过程,程序判断正误。
正确结果:
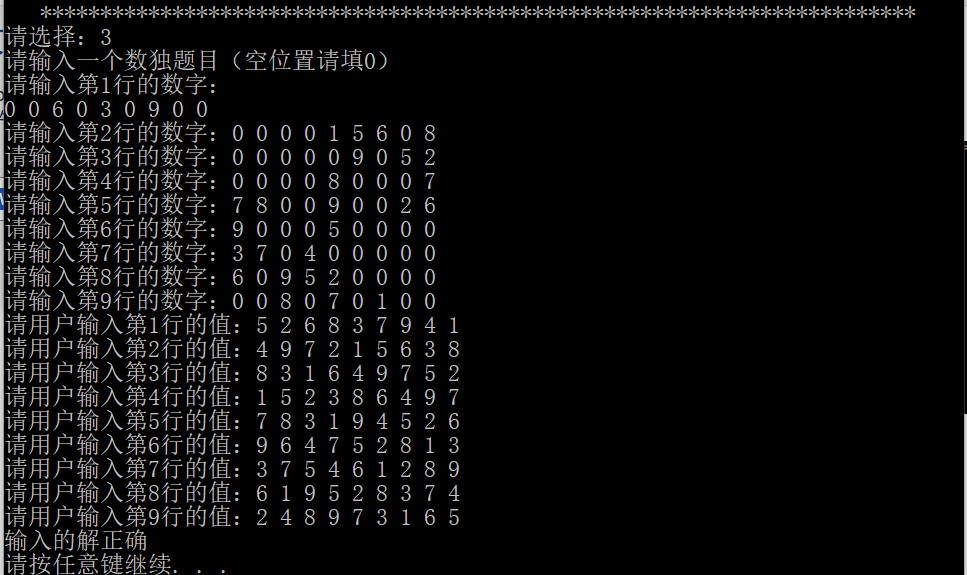
错误结果:

7.4 程序出题,输入答案
程序会生成题目,用户输入答案,如果答案和题目有冲突会给出提示。
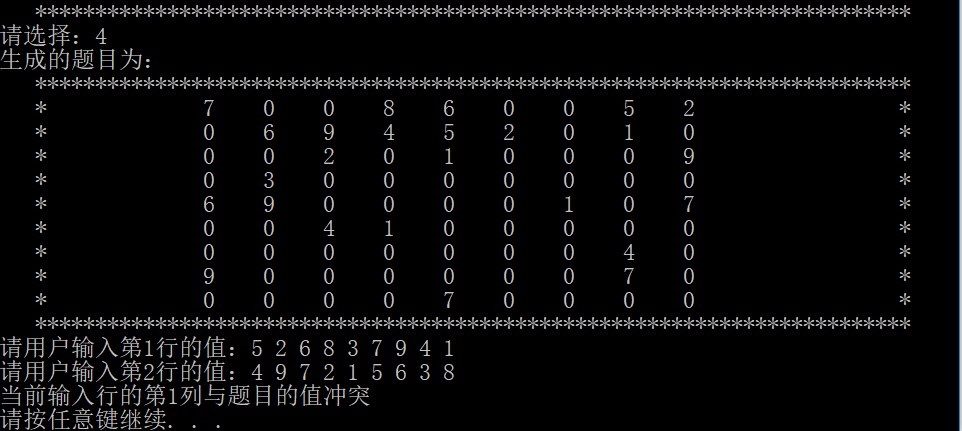
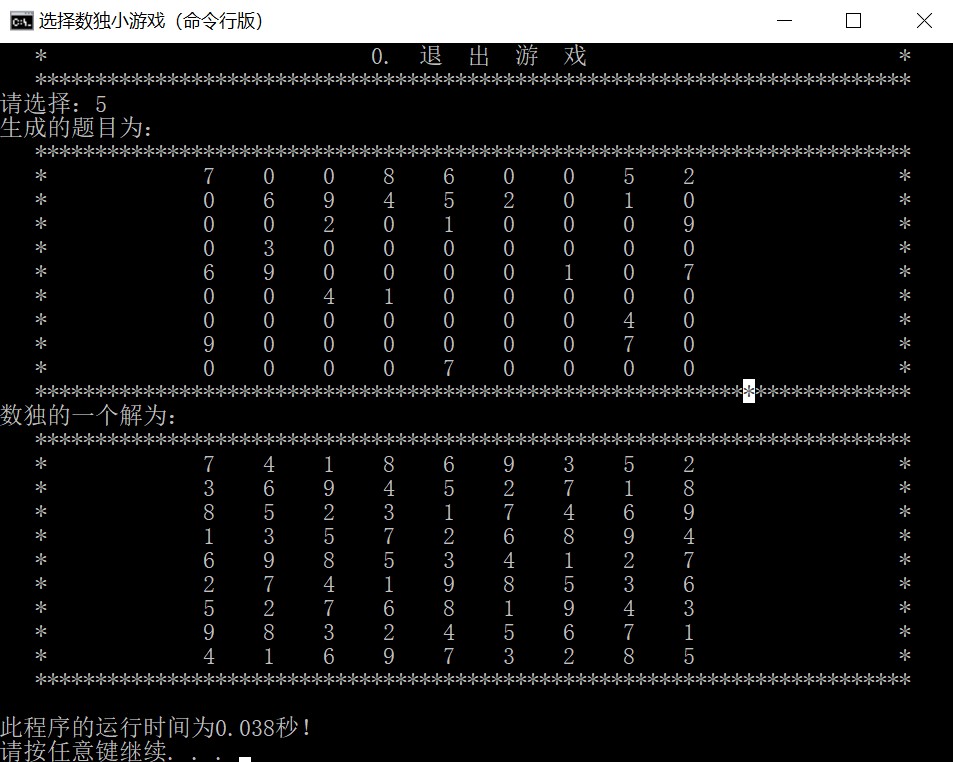
7.5 程序出题,程序求解
程序自动出题,并且完成求解过程给出答案。
7.6 游戏统计数据
给出进行数独游戏的总局数。

7.7 游戏规则介绍
简单介绍游戏规则。

7.8 开发者信息
7.9 退出游戏
倒计时10秒钟退出游戏。


八、图形界面搭建
在命令行版本的基础上搭建图形界面。
我们使用第三方图形库ege来搭建图形界面。
使用图形库编程,基本思想就是根据用户的操作在屏幕上画出对应的文字或图像。本程序屏幕刷新的频率为80帧。
8.1 鼠标事件和键盘事件
每一帧都要判断当前是否有鼠标消息,有则读取一个鼠标消息,进行进一步的判断和操作。键盘事件同理。
8.2 基本元素的绘制
通过画直线(line函数)、放图片(putimage函数)、放文字(outtextrect函数)三个基本功能绘制图像。
8.3 点击功能
在鼠标的mouse_msg_down事件中,根据鼠标的位置来判断用户点击了哪一个选项,然后执行对应的功能。
8.4 鼠标拖拽功能
用户可以使用鼠标拖拽数字到81个格子里。在mouse_msg_down事件中,通过鼠标位置判断用户是否按住了数字图片以及按住了哪一个数字图片,使用变量flag=1标记按住了数字图片,使用变量index记录按住了哪一个图片。每一帧都判断flag是否等于1,等于1则在鼠标的位置显示对应index的图片。在mouse_msg_up事件中,根据鼠标位置计算当前所在行和列,进而计算应该绘制图片的坐标,需要绘制的图片的坐标、数字存入变量InfOfImage node中,如果鼠标的位置在81个格子的范围内则将node插入vector v中。每一帧都要根据vector内的信息绘制图片,并将对应的数字通过数独类的Insert函数插入到数独中。图片可以覆盖,但不能删除。
8.5 键盘输入功能
鼠标单击某一个格子,然后通过键盘输入数字,格子就会显示对应的图片。在mouse_msg_down事件中,根据鼠标位置计算当前行和列的位置,赋值给变量currentRow和currentCol。在键盘的输入事件中,如果字符为大于’0’小于等于’9’的字符,则求出应该画图的坐标,将对应的信息存入变量InfOfImage node,存入vector v中,进而进行绘制和数字的插入。和鼠标拖拽相同,图片可以覆盖,但不能删除。
8.6 打开网页
用户点击开发者信息里的网址,会使用默认浏览器打开对应网页。这个功能使用cmd命令实现,命令 start [网址] 即可打开对应网页。
8.7 防止资源被篡改
程序使用了一些外部资源,图片、字体等,使用Init函数判断文件是否存在以及文件大小是否和预设值相等,资源被删除或被篡改则退出程序。
九、图形界面运行测试
9.1 主菜单
主界面有5个选项:电脑求解数独、数独大闯关、游戏规则介绍、关于开发者、退出游戏。

9.2 电脑求解数独
用户构造一个题目,电脑进行求解。
点击电脑求解,即可显示一个答案。
点击清空可以清空所有数字,用户可以再构造一个题目进行求解;点击返回主菜单可以返回主菜单。

9.3 数独大闯关
电脑随机生成一个数独题目,用户进行求解。求解后点击验证正误即可判断是否正确。题目难度会逐渐增大,最初空白部分为1,每做出一道题,题目的空白部分就会增加1.

9.4 游戏规则介绍
简单介绍数独的规则。

9.5 关于开发者
介绍开发者信息

9.6 彩蛋
在关于开发者界面点击“关浩博”会出现彩蛋:laughing:
十、感想与收获
10.1 关浩博
这次项目的开发,增强了我的团队合作意识,积累了团队合作开发项目的经验。增加了对算法的理解,提升了开发较大项目的能力。我负责数独求解算法、搭建图形界面、项目整体把控。我学会了如何管理整个项目,以及项目进度的推进。
10.2 张存涛
通过数独这个项目,我明白了个人与团队协助开发的重要性。首先我们对其进行了需求分析,制定了C++类和所有的函数分析。我是负责求解算法的。首先我先实现了递归回溯的1.0版本。然后分析了递归算法比较耗时,所以用了信息熵求解的优化算法。最后是将所有的代码合在一起进行调试。
通过这次的课程,学会了可以看一些好的论文然后将论文中的算法实现。然后,在完成需求分析后,指定变量和函数申明的应该加以详细的注释,便于组内成员明白具体的细节。
10.3 张迪
在完成数独的过程中,我学会了如何独立发现问题,分析问题,处理问题和解决能力,也学会了如何在合作中成长,相互合作,相互帮助。尤其是在数独算法的求解中,每次的优化算法的实现都是团队心血的见证,看着程序从1.0到3.0再到10.0 ,每一次改进的完成,心中总是有说不出的开心,也正是每一次的进步与更新,让我们更加团结,更加坚定地做下去。在图形化界面的搭建设计上,更是耗费了大量心血,每一张图片,每一行代码都是一个个鲜活的个体,当最终的界面显现出来的时候,就像是一个襁褓中的孩子,开心与欢乐涌上我们的心头。万物皆无味,唯有代码甜。