题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：
每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例：

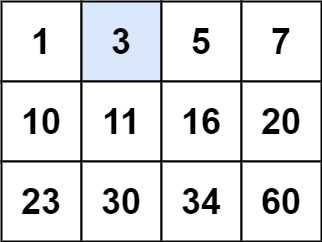
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

题目分析

二分查找

每行从左到右递增，同时每行第一个数字大于上一行最后一个数字。
本质就是一个一维数组折叠成了二维，直接按照一维的模式进行二分查找即可。时间复杂度 O(log(m * n)).

从右上角枚举

如果没有【每行的第一个整数大于前一行的最后一个整数】这个条件，仅仅是每行递增 每列也递增，就不太方便二分查找了。
从左上角出发，会发现每次都面临2个选择，向右或向下。
而从右上角出发，则每次只面临一个选择，可以直接进行遍历，直到找到目标，或跳出网格边界。时间复杂度 O(m + n).

Java

public boolean searchMatrix(int[][] matrix, int target) {
    int m = matrix.length, n = matrix[0].length;
    int size = m * n;
    int left = 0, right = size - 1, mid = 0;
    while (left <= right) {
        mid = (left + right) / 2;
        int cow = mid / n;
        int row = mid % n;
        if (matrix[cow][row] < target) {
            left = mid + 1;
        } else if (matrix[cow][row] > target) {
            right = mid - 1;
        } else {
            return true;
        }
    }
    return false;
}

public boolean searchMatrix2(int[][] matrix, int target) {
    int m = matrix.length, n = matrix[0].length;
    int i = 0, j = n - 1;
    while (i >= 0 && i < m && j >= 0 && j < n) {
        if (matrix[i][j] > target) {
            j--;
        } else if (matrix[i][j] < target) {
            i++;
        } else {
            return true;
        }
    }
    return false;
}

Kotlin

fun searchMatrix(matrix: Array<IntArray>, target: Int): Boolean {
    val m = matrix.size
    val n = matrix[0].size
    val size = m * n
    var left = 0
    var right = size - 1
    while (left <= right) {
        val mid = (left + right) / 2
        val cow = mid / n
        val row = mid % n
        if (matrix[cow][row] < target) {
            left = mid + 1
        } else if (matrix[cow][row] > target) {
            right = mid - 1
        } else {
            return true
        }
    }
    return false
}