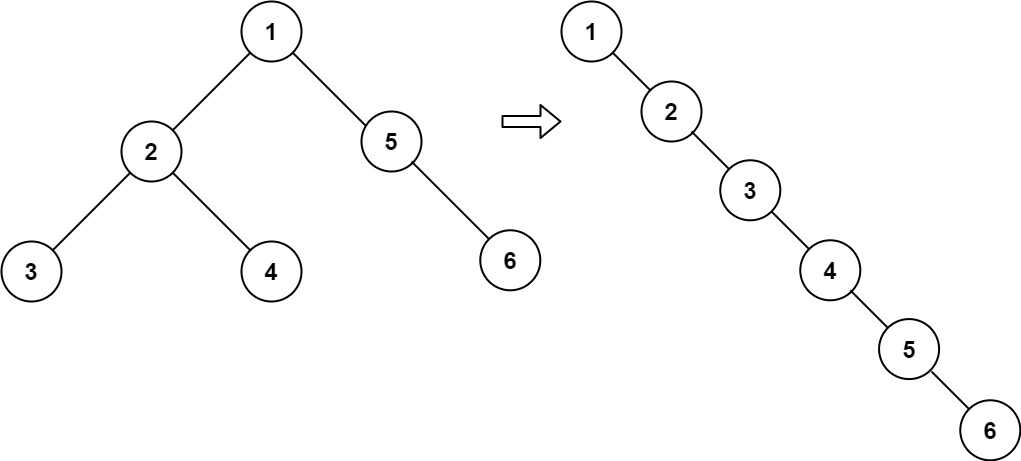
题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

题目分析

先序遍历

先序遍历，可以递归，也可以使用栈模拟。把遍历结果存在 list 中，最后再统一修改结点之间的父子关系。
时间复杂度 O(n)，空间复杂度 O(n)

前驱结点

先序遍历是 根 -> 左 -> 右 的顺序，对于右子结点来说，前驱是根的左子树中最后一个结点。
1. 找到根的左子树的最后一个结点 last，把根的右子树连接到 last 上
2. 把根的左子树移动到右边，变成右子树
3. 向右方处理下一个结点，不断循环

时间复杂度 O(n)，空间复杂度 O(1)

Java

public void flatten(TreeNode root) {
    List<TreeNode> list = new ArrayList<>();
    dfs(root, list);
    for (int i = 1; i < list.size(); i++) {
        TreeNode pre = list.get(i - 1);
        pre.left = null;
        pre.right = list.get(i);
    }
}

private void dfs(TreeNode root, List<TreeNode> list) {
    if (root == null) {
        return;
    }
    list.add(root);
    dfs(root.left, list);
    dfs(root.right, list);
}

public void flatten2(TreeNode root) {
    List<TreeNode> list = new ArrayList<>();
    Deque<TreeNode> stack = new LinkedList<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            list.add(cur);
            cur = cur.left;
        }

        cur = stack.pop();
        cur = cur.right;
    }
    for (int i = 1; i < list.size(); i++) {
        TreeNode pre = list.get(i - 1);
        pre.left = null;
        pre.right = list.get(i);
    }
}

public void flatten3(TreeNode root) {
    TreeNode node = root;
    while (node != null) {
        if (node.left != null) {
            TreeNode leftLast = node.left;
            while (leftLast.right != null) {
                leftLast = leftLast.right;
            }
            leftLast.right = node.right;
            node.right = node.left;
            node.left = null;
        }
        node = node.right;
    }
}

Kotlin

fun flatten(root: TreeNode?): Unit {
    var node = root
    while (node != null) {
        if (node.left != null) {
            var leftLast = node.left
            while (leftLast?.right != null) {
                leftLast = leftLast.right
            }
            leftLast?.right = node.right
            node.right = node.left
            node.left = null
        }
        node = node.right
    }
}