题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例1

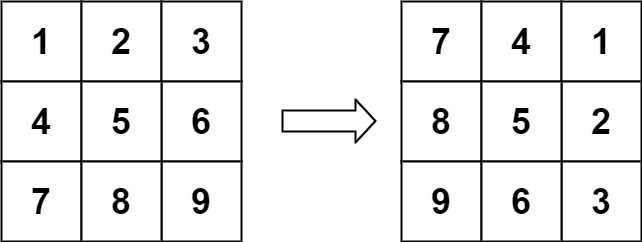
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

题目分析

循环替换

围绕中心点，把矩阵分成4个小矩阵：左上、右上、右下、左下
枚举左上角的小矩阵内的元素，每个元素进行循环旋转，对应4个数字

2步交换

把顺时针旋转拆分成 2 步交换：
– 左上和右下交换一次（延对角线对折）
– 整体上下交换一次（延水平线对折）

Java

public void rotate1(int[][] matrix) {
    int n = matrix.length;
    for(int i = 0; i < n / 2; i++) {
        for(int j = 0; j < (n + 1) / 2; j++){
            int temp = matrix[i][j];
            matrix[i][j] = matrix[n - j - 1][i];
            matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
            matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
            matrix[j][n - i - 1] = temp;
        }
    }
}

public void rotate2(int[][] matrix) {
    int n = matrix.length;
    for (int i = 0; i < n; i++) {
        for (int j = 0; i + j < n; j++) {
            swap(matrix, i, j, n - j - 1, n - i - 1);
        }
    }

    for (int i = 0; i < n / 2; i++) {
        for (int j = 0; j < n; j++) {
            swap(matrix, i, j, n - i - 1, j);
        }
    }
}

private void swap(int[][] matrix, int x1, int y1, int x2, int y2) {
    int temp = matrix[x1][y1];
    matrix[x1][y1] = matrix[x2][y2];
    matrix[x2][y2] = temp;
}

Kotlin

fun rotate1(matrix: Array<IntArray>): Unit {
    val n = matrix.size
    for (i in 0 until n / 2) {
        for (j in 0 until (n + 1) / 2) {
            val temp = matrix[i][j]
            matrix[i][j] = matrix[n - j - 1][i]
            matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
            matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
            matrix[j][n - i - 1] = temp
        }
    }
}

fun rotate2(matrix: Array<IntArray>): Unit {
    val n = matrix.size
    for (i in 0 until n) {
        for (j in 0 until n - i) {
            swap1(matrix, i, j, n - 1 - j, n - 1 - i)
        }
    }
    for (i in 0 until n / 2) {
        for (j in 0 until n) {
            swap1(matrix, i, j, n - i - 1, j)
        }
    }
}

private fun swap1(matrix: Array<IntArray>, x1: Int, y1: Int, x2: Int, y2: Int) {
    val temp = matrix[x1][y1]
    matrix[x1][y1] = matrix[x2][y2]
    matrix[x2][y2] = temp
}