题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例：

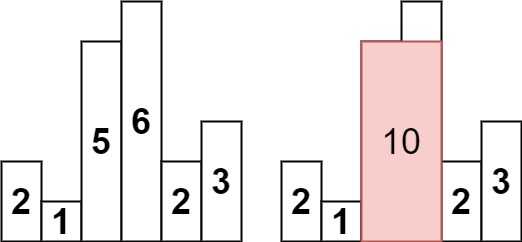
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

题目分析

最大矩形的高一定是某个柱子的高，因此枚举每个柱子，计算以其为高的矩形的最大面积。对于一个柱子来说，以其高度 h 为高的矩形，最大宽度是不断向左/右延伸，直到第一个高度小于 h 的柱子。因此问题转化成了，寻找每个柱子在左侧和右侧的第一个更小的柱子。

可以使用单调栈实现，栈内保持从底到顶递增。每次放入柱子 i 前，先将栈里比自己更高的柱子都移出，在移除过程中计算以被移出柱子为高的最大矩形面积（移除后，新的栈顶柱子的高一定小于被移出柱子的高，所以最大宽度是 i – 栈顶柱子下标 – 1）。

代码中在栈里放入柱子的下标即可，需要时可通过数组读取对应高度。
最后一个柱子，需要额外触发出栈，可以在原数组最右侧增加一个高度为0的柱子，简化代码。
栈底柱子出栈时，需要额外计算左侧的宽度，可以在原数组最左侧增加一个高度为0的柱子，简化代码。

时间复杂度 O(n).

Java

public int largestRectangleArea(int[] heights) {
    int ans = 0;
    Deque<Integer> stack = new LinkedList<>();
    int[] h = new int[heights.length + 2];
    System.arraycopy(heights, 0, h, 1, heights.length);

    for(int i = 0; i < h.length; i++) {
        while(!stack.isEmpty() && h[stack.peek()] > h[i]) {
            int height = h[stack.pop()];
            int width = i - stack.peek() - 1;
            ans = Math.max(ans, width * height);
        }
        stack.push(i);
    }
    return ans;
}

Kotlin

fun largestRectangleArea(heights: IntArray): Int {
    var ans = 0
    val stack = LinkedList<Int>()
    val h = IntArray(heights.size + 2) { i -> if (i in 1..heights.size) heights[i - 1] else 0 }
    for (i in h.indices) {
        while (stack.isNotEmpty() && h[stack.peek()] > h[i]) {
            val height = h[stack.pop()]
            val width = i - stack.peek() - 1
            ans = max(ans, height * width)
        }
        stack.push(i)
    }
    return ans
}